Transformasi

Tranformasi 

A. Refleksi 

Refleksi atau pencerminan merupakan satu jenis transformasi yang memindahkan setiap titik pada suatu bidang dengan mengggunakan sifat bayangan cermin dari titik-titik yang dipindahkan. Perhatikan gambar di bawah.

Gambar di atas menunjukkan contoh refleksi (pencerminan) bangun datar ABCDE pada garis m.

Perhatikan bahwa ruas garis yang menghubungkan titik dan bayangannya tegak lurus terhadap garis m. Garis m disebut garis refleksi untuk ABCDE dan bayangannya A’B’C’D’E’. Karena E terletak pada garis refleksi, titik awal dan bayangannya berada di titik yang sama. Jarak antara A terhadap garis m sama dengan jarak A’ terhadap garis m, begitu pula untuk titik sudut yang lainnya dan bayangannya yang memiliki jarak sama terhadap garis refleksi m.

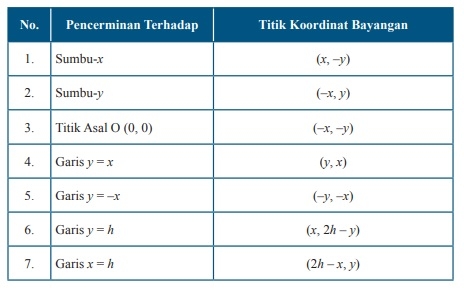
Jika diketahui sebarang titik dengan koordinat (x, y) pada koordinat kartesius, maka koordinat bayangan hasil pencerminannya dapat dilihat pada tabel berikut.

Contoh soal

contoh 1

Titik P (2, 1) dicerminkan terhadap sumbu Y, maka P' adalah...

a. (1, 2)

b. (-1, -2)

c. (-2, 1)

d. (2, 1)

Pembahasan :

Rumus : A (x,y) direfleksikan terhadap sumbu Y hasilnya A' (-x,y)

Jadi P (2,1) direfleksikan terhadap sumbu Y hasilnya P' (-2,1)

Jawaban yang benar adalah C.

Contoh 2

Titik B (3, 2) dicerminkan terhadap sumbu X, maka B' adalah...

a. (2, 3)

b. (-3, -2)

c. (-3, 2)

d. (3, -2)

Pembahasan :

Rumus : A (x,y) direfleksikan terhadap sumbu X hasilnya A' (x,-y)

Jadi B (3,2) direfleksikan terhadap sumbu X hasilnya B' (3,-2)

Jawaban yang benar adalah D

Contoh 3

Bayangan titik P(-4, 5) oleh refleksi terhadap garis y = -x dilanjutkan dengan refleksi terhadap garis x = 2 adalah...

a. P’(-5, 4)

b. P’ (4, -5)

c. P’ (9, 4)

d. P’ (-4, 9)

Pembahasan :

Soal ini kita hanya perlu melakukan dua kali refleksi

Refleksi I garis y = -x

Rumus : A (x,y) direfleksikan terhadap garis y = -x hasilnya A' (-y,-x)

Jadi P (-4,5) direfleksikan terhadap garis y = -x hasilnya P' (-5,4)

Refleksi II garis x = 2

Rumus : A (x,y) direfleksikan terhadap garis x = m hasilnya A' ((2(m)-x), y)

Jadi titik P' (-5,4) direfleksikan terhadap garis x = 2 hasilnya P'' (9, 4)

Jawaban yang benar C

B. Translasi

Translasi merupakan salah satu jenis transformasi yang bertujuan untuk memindahkan semua titik suatu bangun dengan jarak dan arah yang sama.

Translasi pada bidang Kartesius dapat dilukis jika kamu mengetahui arah dan seberapa jauh gambar bergerak secara mendatar dan atau vertikal. Untuk nilai yang sudah ditentukan a dan b yakni translasi 

memindahkan setiap titik P  (x, y) dari sebuah bangun pada bidang datar ke P' (x + a, y + b). Translasi dapat disimbolkan dengan (x, y) --> (x + a, y + b).

Contoh soal 

Contoh 1

Titik A (7, -6) ditranslasikan oleh T = (-2, 4), maka koordinat titik A’ adalah...

a. (9, -10)

b. (-5, -2)

c. (5, -2)

d. (-9, 10)

Pembahasan :

Rumus : A (x,y) ditanslasikan terhadap titik (a,b) hasilnya A' ((x + a), (y + b))

Jadi A (7,-6) ditanslasikan terhadap titik (-2,4) hasilnya A' (5, -2)

Jawaban yang benar C

Contoh 2

Jika titik G'(4, -1) adalah bayangan titik dari G (7, -5) oleh translasi T, maka nilai T adalah ...

a. (2, 5)

b. (-3, 4)

c. (1, 7)

d. (4, 2)

Pembahasan :

Soal ini meminta kita untuk mencari nilai koordinat translasi yaitu nilai a dan nilai b

x + a = 4 (nilai 4 diambil dari hasil translasi koordinat x; G'(4, -1) )

7 + a = 4 (nilai 7 diambil dari koordinat awal x; G'(4, -1) )

a = 4 - 7

a = -3

y + b = -1 (nilai -1 diambil dari hasil translasi koordinta y ; G (7, -5) )

-5 +  b = -1 (nilai -5 diambil dari koordinat awal y ; G (7, -5) )

b = -1 + 5

b = 4

Jadi T (a,b) = T (-3,4)

Jawaban yang benar B

Contoh 3

Jika garis 3x – 2y = 6 ditranslasikan oleh T = (3, -4) maka bayangan garis tersebut adalah...

a. 3x – 2y = 6

b. 3x – 2y = 3

c. 3x – 2y = -11

d. 3x – 2y = 23

Pembahasan :

x' = (x + 3)

y' = (y – 4)

3x' – 2y' = 6

3(x + 3) – 2 (y – 4) = 6

3x + 9 – 2y + 8 = 6

3x – 2y + 17 = 6

3x – 2y = 6 – 17

3x -  2y = -11

Jawaban yang benar C.

C. Rotasi 

Rotasi merupakan salah satu bentuk transformasi yang memutar setiap titik pada gambar sampai sudut dan arah tertentu terhadap titik yang tetap. Titik tetap ini disebut pusat rotasi. Besarnya sudut dari bayangan benda terhadap posisi awal disebut dengan sudut rotasi. 

• Untuk rotasi searah jarum jam, sudut diberi tanda negatif (–)

• Untuk rotasi berlawanan arah jarum jam, sudut diberi tanda positif (+)

Brikut merupakan rumus praktis dari rotasi dengan pusat rotasi (0,0)

 

Contoh soal 

Contoh 1

titik P (8, 5) dirotasikan sejauh 90° terhadap titik pusat O (0, 0) berlawanan arah jarum jam. Nilai P' adalah...

a. (5, 8)

b. (-8, 5)

c. (-8, -5)

d. (-5, 8)

Pembahasan :

Rumus : A (x,y) dirotasi sebesar 90° pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-y, x)

Jadi P (8,5) dirotasi 90° pusat rotasi (0,0) hasilnya P' (-5, 8)

Jawaban yang benar D

Contoh 2

Bayangan dari titik A(-2, 3) yang dirotasikan sebesar 90° berlawanan arah jarum jam adalah...

a. A'(2, -3)

b. A'(3, -2)

c. A'(-3, -2)

d. A'(3, 2)

Pembahasan :

Rumus : A (x,y) dirotasi sebesar 90° pusat rotasi (a,b) dan titik asal (x,y) hasilnya A' (-y, x)

Jadi A (-2,3) dirotasi 90° pusat rotasi (0,0) hasilnya A' (-3, -2)

Jawaban yang benar C

Contoh 3

Persamaan bayangan garis 3x – y + 2 = 0 yang dicerminkan terhadap garis y = x kemudian dilanjutkan dengan rotasi 90° terhadap titik asal adalah...

a. 3x + y + 2 = 0

b. 3x – y – 2 = 0

c. 3y – x + 2 = 0

d. x – 3y – 2 = 0

Pembahasan :

Soal ini meminta kita melakukan dua langkah transformasi, pertama pencerminan kemudian hasil pencerminan dirotasi.

Pencerminan (refleksi) terhadap garis y = x

Rumus : A (x,y) direfleksikan terhadap garis y = x hasilnya A' (y,x)

x' = y

y' = x

3x' – y' + 2 = 0

3y – x + 2 = 0

Perputaran (rotasi) 90° terhadap titik asal

Rumus : A (x,y) dirotasi sebesar 90° pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-y, x)

x' = -y

y' = x

3y' – x' + 2 = 0

3(x) – (-y) + 2 = 0

3x + y + 2 = 0

Jawaban yang benar A

Contoh 4

Titik A (-3, 6) dirotasikan dengan pusat di O(0, 0) sebesar 180°, maka bayangan koordinat titik A adalah..

a. (9-3, -6)

b. (3, -6)

c. (-6, -3)

d. (-6, 3)

Pembahasan :

Rumus : A (x,y) dirotasi sebesar 1800 pusat rotasi (0,0) dan titik asal (x,y) hasilnya A' (-x, -y)

Jadi A (-3,6) dirotasi 180° pusat rotasi (0,0) hasilnya A' (3, -6)

Jawaban yang benar B

D. Dilatasi 

Dilatasi terhadap titik pusat merupakan perkalian dari koordinat tiap-tiap titik pada suatu bangun datar dengan faktor skala sebesar k. Faktor skala menentukan apakah suatu dilatasi merupakan pembesaran atau pengecilan. Secara umum dilatasi dari suatu koordinat (x, y) dengan faktor skala k akan menghasilkan koordinat (kx, ky) atau dapat ditulis (x, y) --> (kx, ky).

Ketika k > 1 maka dilatasi tersebut termasuk ke dalam pembesaran, tetapi jika 0 < k < 1 maka dilatasi tersebut termasuk ke dalam pengecilan. Untuk memperbesar atau memperkecil bangun, letak pusat dilatasi dapat di dalam, di luar, atau pada tepi bangun yang akan didilatasikan.

Contoh soal 

Contoh 1

Koordinat bayangan titik C (9, -6) didilatasi terhadap titik pusat O dengan faktor skala – 1/3 adalah ...

a. (-2, 3)

b. (2, 3)

c. (3, 2)

d. (-3, 2)

Pembahasan :

Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)

Jadi C (9,-6) didilatasi dengan pusat (0,0) faktor skala -1/3 hasilnya C' (-3, 2)

Jawaban yang benar D

Contoh 2

titik Q (3, -6) didilatasi terhadap titik pusat M (-2, 3) dengan faktor skala 2, maka bayangan titik Q adalah...

a. (7, 10)

b. (8, -15)

c. (-3, -7)

d. (-6, 8)

Pembahasan :

Rumus : A (x,y) didilatasi dengan pusat (a,b) faktor skala k titik asal (x,y) hasilnya A' (k(x - a) + a, k(y - b)+b)

Jadi Q (3,-6) didilatasi dengan pusat M (-2,3) faktor skala 2 hasilnya Q' (8,-15)

Nilai 8 diambil dari 

x' = k (x - a) + a dimana k = 2, x = 3, dan a = -2

x' = 2 (3 - (-2)) + -2 = 10 - 2 = 8

Nilai -15 diambil dari

y' = k (y - b) + b dimana k =2, y = -6, dan b = 3

y' = 2 (-6 - 3) + 3 = -18 + 3 = -15

Jawaban yang benar B

Contoh 3

Bayangan titik P (-2, 3) oleh dilatasi [O, k] adalah P’(4, -6), sehingga bayangan titik Q (3, -2) oleh dilatasi [O, 4k] adalah...

a. (-24, 16)

b. (24, -16)

c. (-24, -16)

d. (24, 16)

Pembahasan :

Soal ini agak berbeda dengan soal-soal sebelumnya, di sini kita terlebih dulu harus memahami maksud dari soal. Biasanya soal seperti ini kita akan bingung karena kita tidak melihat dengan jelas faktor skala dan pusat dilatasi. Padahal sebenarnya faktor skala dan pusat dilatasi ada hanya dituliskan dalam bentuk lain yaitu [0,k]. Berarti soal ini faktor skalanya adalah k dan pusat dilatasi (0,0)

Untuk menyelesaikan soal ini terlebih dahulu kita mencari faktor skalanya

Rumus : Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)

Dari data P (-2,3) dan P' (4,-6) serta [0,k] kita bisa menentukan besar nilai k

Jadi x' = kx dan y' = ky dan nilai x' = 4, y' = -6, x = -2, dan y = 3, sehingga

4 = k . -2

k = 4/-2

k = -2

Sekarang kita bisa mencari Q (3, -2) oleh dilatasi [O, 4k] karena kita sudah memiliki nilai k = -2

Faktor skala untuk dilatasi Q adalah 4k, berarti nilai faktor skala untuk Q adalah k = -8

Rumus : Rumus : A (x,y) didilatasi dengan pusat (0,0) faktor skala k titik asal (x,y) hasilnya A' (kx, ky)

Jadi Q (3,-2) didilatasi dengan pusat (0,0) faktor skala -8 hasilnya Q' (-24,16)

Jawaban yang benar adalah A

Contoh 4

Diketahu titik P (12, -5) dan A (-2, 1). Bayangan titik P oleh dilatasi [A, ½ ] adalah...

a. P' (-2, 5)

b. P' (2, 5)

c. P' (5, -2)

d. P' (-5, -2)

Pembahasan :

Rumus : A (x,y) didilatasi dengan pusat (a,b) faktor skala k titik asal (x,y) hasilnya A' (k(x - a) + a, k(y - b)+b)

x ' = 1/2 (12 - (-2)) + (-2) = 5

y' = 1/2 (-5 - 1) + 1 = 2

Jadi P (12,-5) didilatasi dengan pusat (-2,1) faktor skala 1/2 hasilnya Q' (5,-2)

Jawaban yang benar adalah C